Using real-world patterns to improve matching in theory and practice

A research publication authored by Tenindra Abeywickrama (Grab), Victor Liang (Grab) and Kian-Lee Tan (NUS) based on their work, which was awarded the Best Scalable Data Science Paper Award for 2021.

Matching the right passengers to the right driver-partners is a critically important task in ride-hailing services. Doing this suboptimally can lead to passengers taking longer to reach their destinations and drivers losing revenue. Perhaps, the most challenging of all is that this is a continuous process with a constant stream of new ride requests and new driver-partners becoming available. This makes computing matchings a very computationally expensive task requiring high throughput.

We discovered that one component of the typically used algorithm to find matchings has a significant impact on efficiency that has hitherto gone unnoticed. However, we also discovered a useful property of real-world optimal matchings that allows us to improve the algorithm, in an interesting scenario of practice informing theory.

A real-world example

Let us consider a simple matching algorithm as depicted in Figure 1, where passengers and driver-partners are matched by travel time. In the figure, we have three driver-partners (D1, D2, and D3) and three passengers (P1, P2, and P3).

Finding the travel time involves computing the fastest route from each driver-partner to each passenger, for example the dotted routes from D1 to P1, P2 and P3 respectively. Finding the assignment of driver-partners to passengers that minimise the overall travel time involves representing the problem in a more abstract way as a bipartite graph shown below.

In the bipartite graph, the set of passengers and the set of driver-partners form the two bipartite sets, respectively. The edges connecting them represent the travel time of the fastest routes, and their costs are shown in the cost matrix on the right.

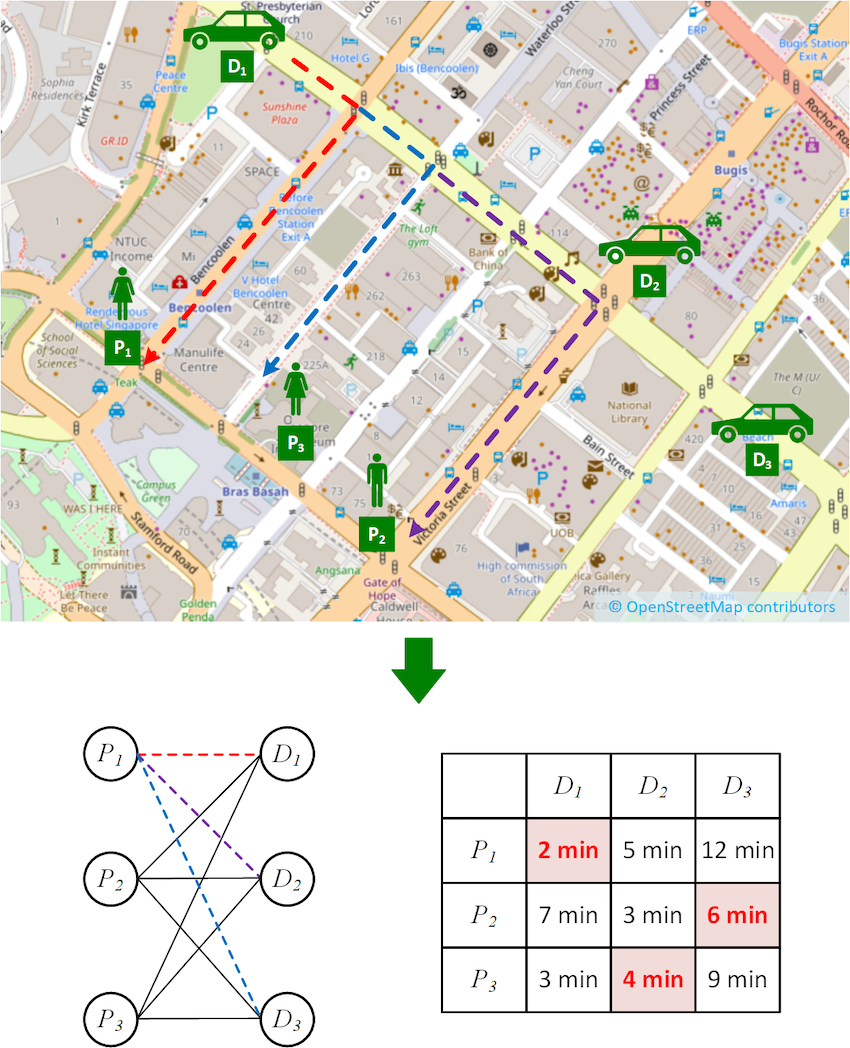
Finding the optimal assignment is known as solving the minimum weight bipartite matching problem (also known as the assignment problem). This problem is often solved using a technique called the Kuhn-Munkres (KM) algorithm¹ (also known as the Hungarian Method).

If we were to run the algorithm on the scenario shown in Figure 1, we would find the optimal matching highlighted in red on the cost matrix shown in the figure. However, there is an important step that we have not paid great attention to so far, and that is the computation of the cost matrix. As it turns out, this step has quite a significant impact on performance in real-world settings.

Impact of the cost matrix

Past work that solves the assignment problem assumes the cost matrix is given as input, but we observe that the time taken to compute the cost matrix is not always trivial. This is especially true in our real-world scenario. Firstly, matching driver-partners and passengers is a continuous process, as we mentioned earlier. Costs are not fixed; they change over time as driver-partners move and new passenger requests are received.

This means the matrix must be recomputed each time we attempt a matching (for example every X seconds). Not only is finding the shortest path between a single passenger and driver-partner computationally expensive, we must do this for all pairs of passengers and driver-partners. In fact, in the real world, the time taken to compute the matrix is longer than the time taken to compute the optimal assignment! A simple consideration of time complexity suggests that this is true.

If m is the number of driver-partners/passengers we are trying to match, the KM algorithm typically runs in O(m^3). If n is the number of nodes in the road network, then computing the cost matrix runs in O(m x n log n) using Dijkstra’s algorithm².

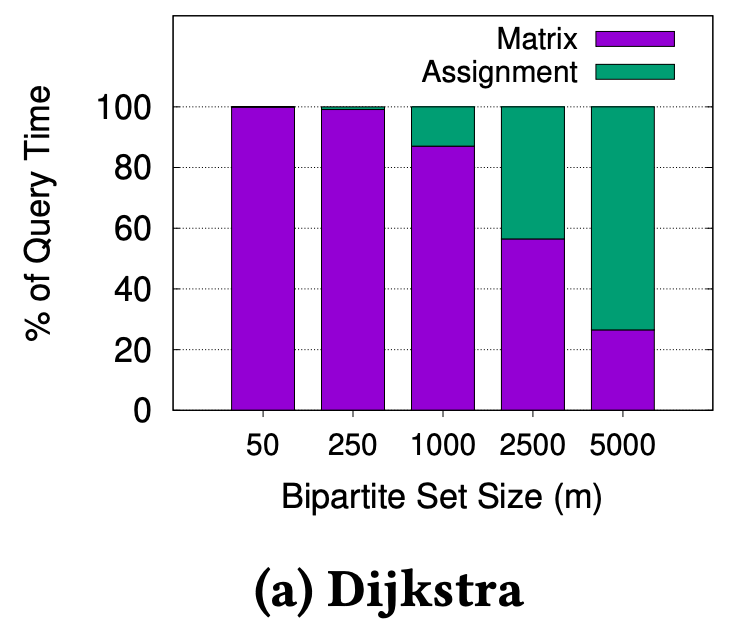
We know that n is around 400,000 for Singapore’s road network (and much larger for bigger cities), thus we can reasonably expect O(m x n log n) to dominate O(m^3) for m < 1500, which is the kind of value for m we expect in the real-world. We ran experiments on Singapore’s road network to verify this, as shown in Figure 2.

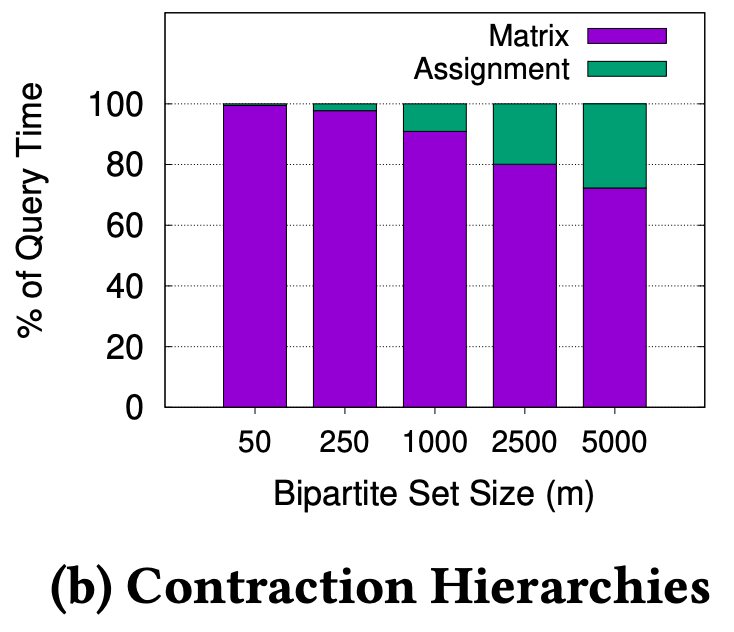In Figure 2a, we can see that m must be greater than 2500, before the assignment time overtakes the matrix computation time. Even if we use a modern and advanced technique like Contraction Hierarchies³ to compute the fastest path, the observation holds, as shown in Figure 2b. This shows we can significantly improve overall matching performance if we can reduce the matrix computation time.

A redeeming intuition: Spatial locality of matching

While studying real-world locations of passengers and driver-partners, we observed an interesting property, which we dubbed “spatial locality of matching”. We find that the passenger assigned to each driver-partner in an optimal matching is one of the nearest passengers to the driver-partner (it might not be the nearest). This makes intuitive sense as passengers and driver-partners will be distributed throughout a city and it’s unlikely that the best match for a particular driver-partner is on the other side of the city.

In Figure 3, we see an example scenario exhibiting spatial locality of matching. While this is an idealised case to demonstrate the principle, it is not a significant departure from the real-world. From the cost matrix shown, it is very easy to see which assignment will give the lowest total travel time.

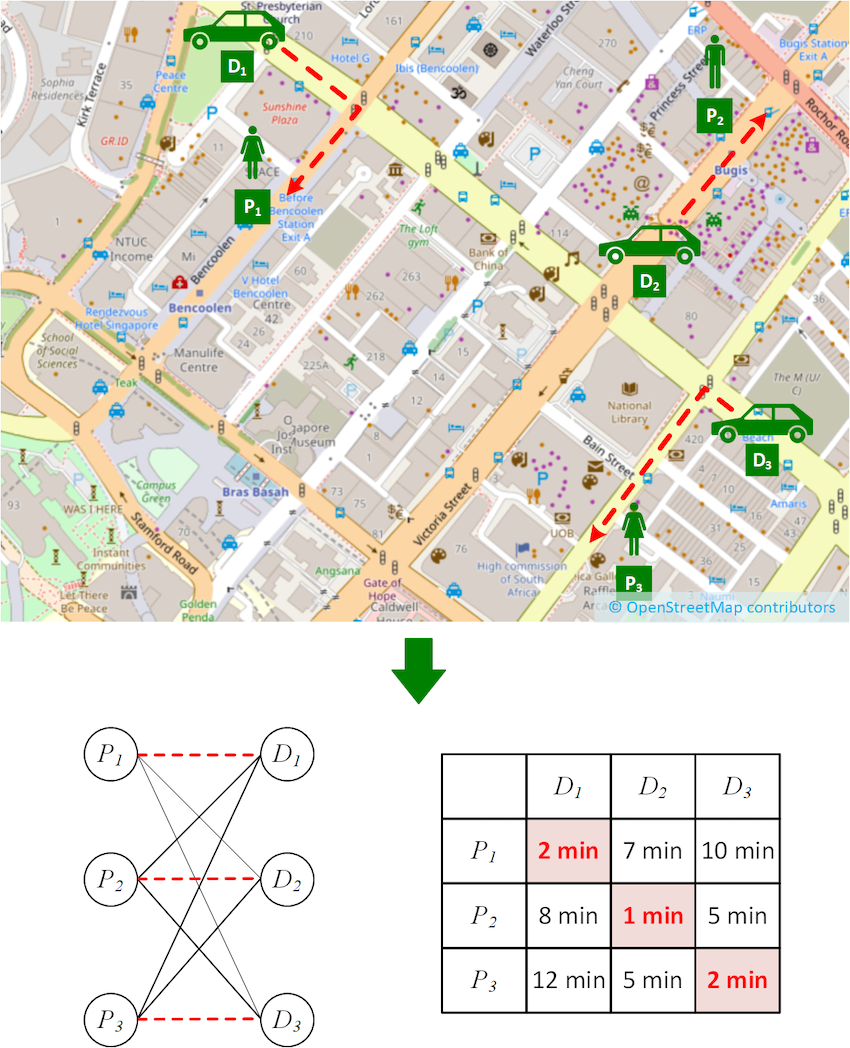
Now, it begs the question, do we even need to compute the other costs to find the optimal matching? For example, can we avoid computing the cost from D3 to P1, which are very far apart and unlikely to be matched?

Incremental Kuhn-Munkres

As it turns out, there is a way to take advantage of spatial locality of matching to reduce cost computation time. We propose an Incremental KM algorithm that computes costs only when they are required, and (hopefully) avoids computing all of them. Our modified KM algorithm incorporates an inexpensive lower-bounding technique to achieve this without adding significant overhead, as we will elaborate in the next section.

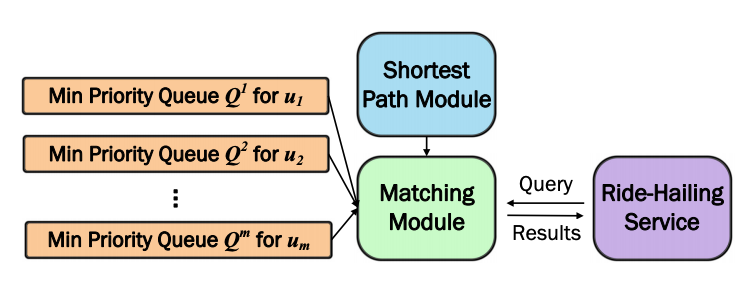
Retrieving objects nearest to a query point by their fastest route is a very well studied problem (commonly referred to as k-Nearest Neighbour search)⁴. We employ this concept to implement a priority queue Qi for each driver ui, as displayed in Figure 4. These priority queues allow retrieving the nearest passengers by a lower-bound on the travel time. The top of a priority queue implies a lower-bound on the travel time for all passengers that have not been retrieved yet. We can then use this minimum lower-bound as a lower-bound edge cost for all bipartite edges associated with that driver-partner for which we have not computed the exact cost so far.

Now, the KM algorithm can proceed as usual, using the virtual edge cost implied by the relevant priority queue, to avoid computing the exact edge cost. Of course, there may be circumstances where the virtual edge cost is insufficiently accurate for KM to compute the optimal matching. To solve this, we propose refinement rules that detect when a virtual edge cost is insufficient.

If a rule is triggered, we refine the queue by retrieving the top element and computing its exact edges; this is where the “incremental” part comes from. In almost all cases, this will also increase the minimum key (lower-bound) in the priority queue.

If you’re interested in finding out more, you can delve deeper into the pruning rules, inner workings of the algorithm and mathematical proofs of correctness by reading our research paper⁵.

For now, it suffices to say that the Incremental KM algorithm produces the exact same result as the original KM algorithm. It just does so in an optimistic incremental way, hoping that we can find the result without computing all possible costs. This is perfectly suited to take advantage of spatial locality of matching. Moreover, not only do we save time by avoiding computing exact costs, we avoid computing longer fastest paths/travel times to further away passengers that are more computationally expensive than those for nearby passengers.

Experimental investigation

Competition

We conducted a thorough experimental investigation to verify the practical performance of the proposed techniques. We implemented two variants of our Incremental KM technique, differing in the implementation of the priority queue and the shortest path technique used.

• IKM-DIJK: Uses Dijkstra’s algorithm to compute shortest paths. Priority queues are simply the priority queue of the Dijkstra’s search from each driver-partner. This adds no overhead over the regular KM algorithm, so any speedup comes for free.
• IKM-GAC: Uses state-of-the-art lower-bound technique COLT⁶ to implement the priority queues and G-tree⁴, a fast technique to compute shortest paths. The COLT index must be built for each assignment, and this overhead is included in all running times.

We compared our proposed variants against the regular KM algorithm using Dijkstra and G-tree, respectively, to compute the entire cost matrix up front. Thus, we can make an apples-to-apples comparison to see how effective our techniques are.

Datasets

We ran experiments using the real-world road network for Singapore. For the Singapore dataset, we also use a real production workload consisting of Grab bookings over a 7-day period from December 2018.

Performance evaluation

To test our technique on the Singapore workload, we created an assignment problem by first choosing the window size W in seconds. Then, we batched all the bookings in a randomly selected window of that size and used the passenger and driver-partner locations from these bookings to create the bipartite sets. Next, we found an optimal matching using each technique and reported the results averaged over several randomly selected windows for several metrics.

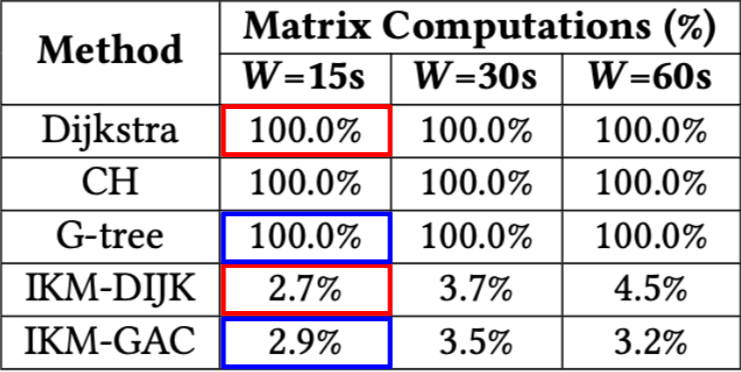
In Figure 5, we verify that our proposed techniques are indeed computing fewer exact costs compared to their counterparts. Naturally, the original KM variants compute 100% of the matrix.

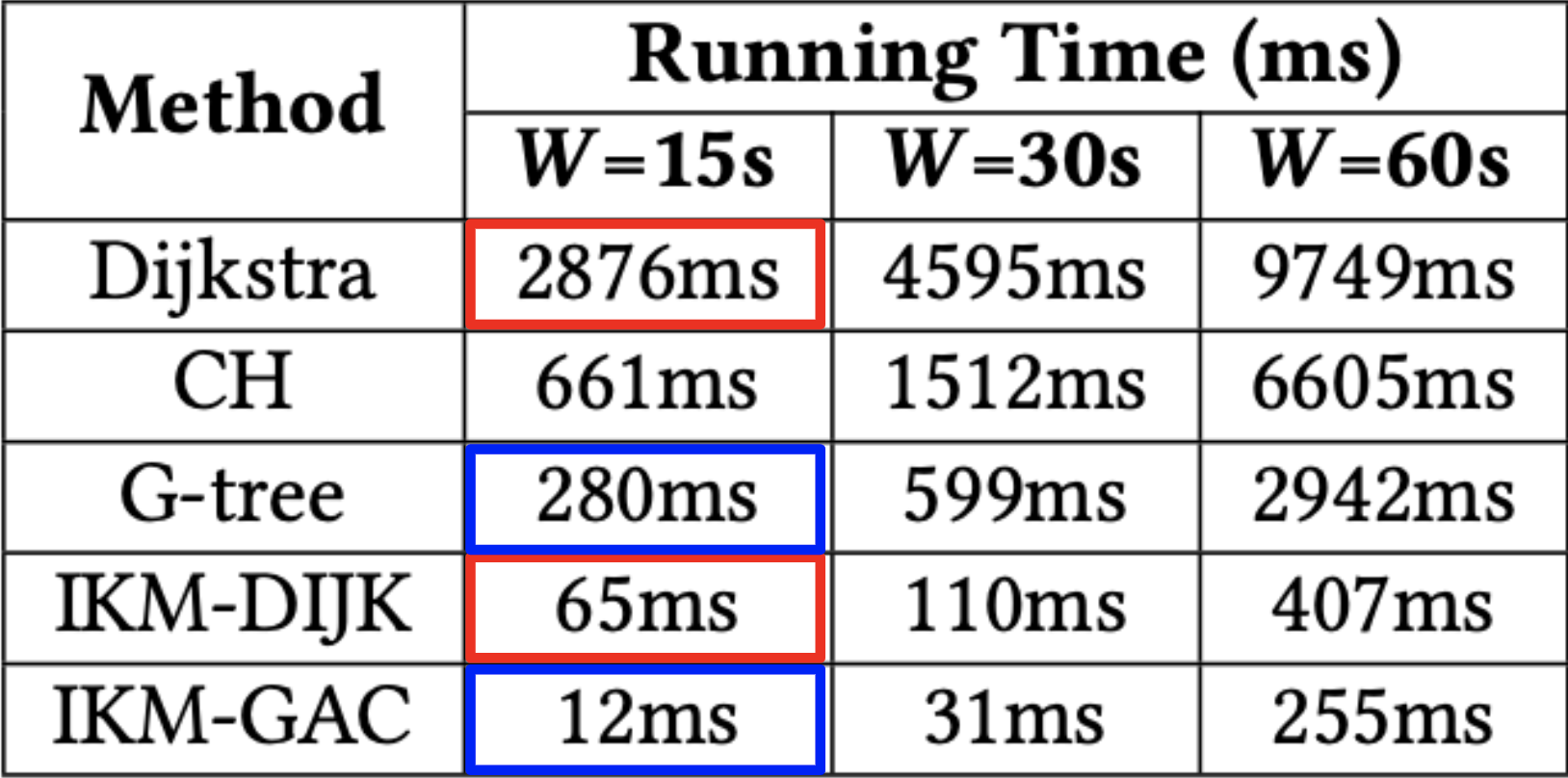
In Figure 6, we can see the running times of each technique. The results in the figure confirm that the reduced computation of exact costs translates to a significant reduction of running time by over an order of magnitude. This verifies that the time saved is greater than any overhead added. Remember, the improvement of IKM-DIJK comes essentially for free! On the other hand, using IKM-GAC can achieve very low running times.

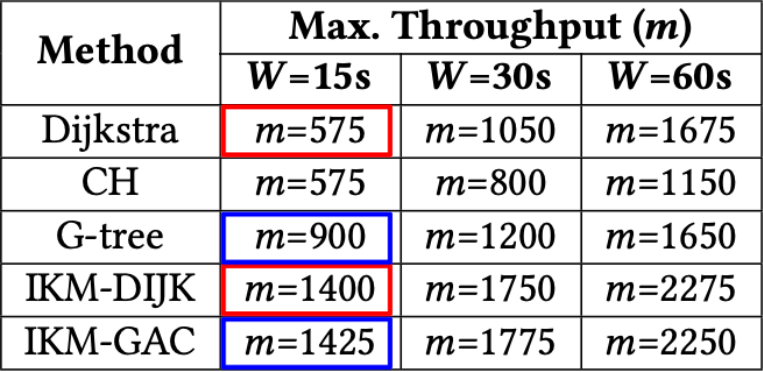
In Figure 7, we report a slightly different metric. We measure m, the maximum number of passengers/driver-partners that can be batched within the time window W. This can be considered as the maximum throughput of each technique. Our technique supports significantly higher throughput.

Note that the improvement is smaller than in other cases because real-world values of m rarely reach these levels, where the assignment time starts to take up a greater proportion of the overall computation time.

Conclusion

In summary, computing assignment costs do indeed have a significant impact on the running time of finding optimal assignments. However, we show that by utilising the spatial locality of matching inherent in real-world assignment problems, we can avoid computing exact costs, unless absolutely necessary, by modifying the KM algorithm to work incrementally.

We presented an interesting case where practice informs the theory, with our novel modifications to the classical KM algorithm. Moreover, our technique can be potentially applied beyond driver-partner and passenger matching in ride-hailing services.

For example, the Route Inspection algorithm also uses shortest path edge costs to find a minimum-weight bipartite matching, and our technique could be a drop-in replacement. It would also be interesting to see if these principles can be generalised and applied to other domains where the assignment problem is used.

Acknowledgements

This research was jointly conducted between Grab and the Grab-NUS AI Lab within the Institute of Data Science at the National University of Singapore (NUS). Tenindra Abeywickrama was previously a postdoctoral fellow at the lab and now a data scientist with Grab.

Special thanks to Kian-Lee Tan from NUS for co-authoring this paper.

Join us

Grab is a leading superapp in Southeast Asia, providing everyday services that matter to consumers. More than just a ride-hailing and food delivery app, Grab offers a wide range of on-demand services in the region, including mobility, food, package and grocery delivery services, mobile payments, and financial services across over 400 cities in eight countries.

Powered by technology and driven by heart, our mission is to drive Southeast Asia forward by creating economic empowerment for everyone. If this mission speaks to you, join our team today!

References